



Vor: Besprechung der Kapitel
Aufwärts: Rezension Physik unter Verwendung
Zurück: Zusammenfassung
Der Virialsatz:
 |
(1) |
für eine homogene Potentialfunktion vom Grad s und für den bekanntesten Fall
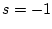 (Gravitation, Coulomb)
(Gravitation, Coulomb)
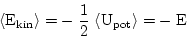 |
(2) |
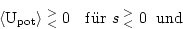 |
(3) |
Abbildung 1:
Zum Virialsatz: Energieerwartunswerte als Funktion des Grades s der homogenen Potentialfunktion, bei auf 1 normierter Gesamtenergie, oder die Vorzeichen der kinetischen, potentiellen und Gesamtenergie
|
|
Das Buch des Autors Physik unter Verwendung des Virialsatzes ist durch seine Arbeiten bei der
Plasmaspektroskopie
in einer Arbeitsgruppe unter Werner Heisenberg im Institut in
München entstanden. Aufmerksam auf dieses Themengebiet wurde er
durch
Schwierigkeiten in der wiederholten Herleitung von mathematischen
Hilfsmitteln,
die er für seine Arbeit benötigte.
Als Hauptthese könnte gelten:
Vormals als frei betrachtete Elektronen werden als gebundene, aber
nicht
an einen einzelnen Kern gebundene, betrachtet. Was als
Einschränkung erscheint, erweist sich als physikalischer
Freiraum.
In einem Festkörper nicht an einen einzelnen Kern gebundene
Elektronen
sind leitend! (,,Bei der üblichen Behandlung entarteter Materie
geht
man zur Bestimmung des Entartungsparameters von einer integrierten
Gleichung (27)(2)
(3') in C.[1] als Normierungsbedingung aus, indem man die Elektronendichte
 vorgibt
und die Elektronen somit als frei definiert. (Man begründet diesen
Vorgang
z.B. mit der Evidenz von Leitungselektronen oder in der
Astrophysik mit der
Annahme, daß der in äußeren Zonen des Sternes erreichte
Ionisationsgrad zum Innern hin nicht geringer werden könne. Solche
Sprechweise
drückt aus, daß es für entartete Materie keine Definition
der Begriffe frei und gebunden gibt. Offensichtlich haben aber die
Begriffe
,,frei`` und ,,leitfähig`` a priori nichts miteinander zu tun.``)
Leitende
Elektronen dichter Plasmen müssen als gebunden betrachtet
werden. C. S. 98 [1]
vorgibt
und die Elektronen somit als frei definiert. (Man begründet diesen
Vorgang
z.B. mit der Evidenz von Leitungselektronen oder in der
Astrophysik mit der
Annahme, daß der in äußeren Zonen des Sternes erreichte
Ionisationsgrad zum Innern hin nicht geringer werden könne. Solche
Sprechweise
drückt aus, daß es für entartete Materie keine Definition
der Begriffe frei und gebunden gibt. Offensichtlich haben aber die
Begriffe
,,frei`` und ,,leitfähig`` a priori nichts miteinander zu tun.``)
Leitende
Elektronen dichter Plasmen müssen als gebunden betrachtet
werden. C. S. 98 [1]




Vor: Besprechung der Kapitel
Aufwärts: Rezension Physik unter Verwendung
Zurück: Zusammenfassung
dexter
2005-10-31
[roomsixhu]
![\includegraphics[width=\textwidth]{clausius.ps}](img7.png)
![]() vorgibt
und die Elektronen somit als frei definiert. (Man begründet diesen
Vorgang
z.B. mit der Evidenz von Leitungselektronen oder in der
Astrophysik mit der
Annahme, daß der in äußeren Zonen des Sternes erreichte
Ionisationsgrad zum Innern hin nicht geringer werden könne. Solche
Sprechweise
drückt aus, daß es für entartete Materie keine Definition
der Begriffe frei und gebunden gibt. Offensichtlich haben aber die
Begriffe
,,frei`` und ,,leitfähig`` a priori nichts miteinander zu tun.``)
Leitende
Elektronen dichter Plasmen müssen als gebunden betrachtet
werden. C. S. 98 [1]
vorgibt
und die Elektronen somit als frei definiert. (Man begründet diesen
Vorgang
z.B. mit der Evidenz von Leitungselektronen oder in der
Astrophysik mit der
Annahme, daß der in äußeren Zonen des Sternes erreichte
Ionisationsgrad zum Innern hin nicht geringer werden könne. Solche
Sprechweise
drückt aus, daß es für entartete Materie keine Definition
der Begriffe frei und gebunden gibt. Offensichtlich haben aber die
Begriffe
,,frei`` und ,,leitfähig`` a priori nichts miteinander zu tun.``)
Leitende
Elektronen dichter Plasmen müssen als gebunden betrachtet
werden. C. S. 98 [1]